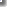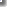"Regardons de plus près les deux géométries non euclidiennes. Dans celle de Lobatchevski, que le langage technique appelle géométrie hyperbolique, il existe un nombre infini de parallèles. Dans celle de Riemann, appelée géométrie elliptique, il n’y a aucune parallèle. Comment une géométrie peut-elle se constituer sans droites parallèles ? Nous pouvons le comprendre par l’intermédiaire d’un modèle qui n’est pas exactement identique à celui d’une géométrie elliptique, mais qui en est un parent proche : un modèle de géométrie sphérique. Ce modèle consiste simplement en la surface d’une sphère. Nous décidons de regarder cette surface comme analogue à un plan.
  Les lignes droites d’un plan sont ici représentées par les « grands cercles » de la sphère. En termes plus généraux, nous disons que dans toute géométrie non euclidienne les lignes qui correspondent aux droites euclidiennes sont des « lignes géodésiques ». Elles ont en commun avec les droites la propriété qui consiste à être le plus court chemin d’un point à un autre.
[...]
  Il faut prendre garde à ne pas exagérer la portée de cette analogie entre le plan riemannien et la surface d’une sphère : en effet, dans l’espace riemannien, deux droites sur un plan n’ont qu’un seul point commun, tandis que les lignes qui sur une sphère correspondent à des droites, les grands cercles, se coupent toujours deux fois. Prenons par exemple deux méridiens : ils se rencontrent au pôle Nord et au pôle Sud. Strictement parlant, notre modèle ne correspond à un plan riemannien que si nous nous restreignons à une partie de la surface de la sphère qui ne contienne pas de points diamétralement opposés comme le sont les pôles."

Rudolf Carnap, Les Fondements philosophiques de la physique, Armand Colin, 1973, p. 131–133.

  "Un modèle particulièrement simple, dû à Félix Klein (1849-1925), de la géométrie non euclidienne est le suivant.

Dans ce modèle là les points de la géométrie sont les points du plan qui sont à l'intérieur d'une ellipse. On exclut tous les points qui sont à l'extérieur de l'ellipse. Les droites sont les intersections des droites ordinaires avec l'intérieur de l'ellipse. Maintenant, il est évident dans ce modèle que le cinquième postulat d'Euclide, que l'on peut reformuler comme l'unicité de la parallèle à une droite donnée passant par un point donné, n'est pas valable. En effet, par un point (par exemple le point I de la figure) extérieur à une droite (la droite AB de la figure), on peut faire passer plusieurs droites L = PQ et L' = RS qui ne la rencontrent pas. Se donner les points et les droites ne suffit pas pour spécifier la géométrie d'Euclide. Il faut pour cela spécifier la relation de congruence entre deux segments AB et CD, ou plus simplement spécifier la longueur d'un segment AB. En l'occurrence, dans le modèle de Klein, cette longueur est donnée par le logarithme du bi-rapport des quarre points (A, B ; b, a), où a et b sont les points d'intersection de la droite AB avec l'ellipse, on spécifie de manière analogue les angles entre deux droites L= PQ et L'= RS.
  Tous les axiomes d'Euclide sont vérifiés par cette géométrie sauf le cinquième axiome. Cette géométrie a été découverte [par Lobatchevski et Bolyai]  au début du XX^e siècle après bien des essais infructueux pour démontrer le cinquième axiome comme conséquence des autres axiomes d'Euclide. Il est frappant de constater l'extraordinaire fécondité de cette question qui aurait pu naïvement apparaître comme un pinaillage de mathématicien.
  Gauss avait fait cette découverte indépendamment mais ne l'avait pas publiée. Loin d'être un simple contre-exemple ésotérique, il s'agissait en fait d'un objet d'une très grande richesse et fécondité, qui a conduit les mathématiciens à sortir du cadre traditionnel de la géométrie euclidienne."

Alain Connes, "L'espace du mathématicien", in Les espaces de l'homme, Odile Jacob, 2005, p. 17-19.
 

Retour au menu sur la démonstration

Retour au menu sur l'espace